Аннотация
В работe [1,c.9], для аппроксимации событий, предшествующих катастрофе, предложено следующая функция от времени: Комплексификация этой формулы и замена переменных позволили вскрыть степенную сущность представленной аппроксимации и определить линейное дифференциальное уравнение, решением которого она является.
Abstract
In work [1,c.9], for aproximation of occasions, preceding the catastrophe, is offered following function from a time: Complexification of this formula and change of variable allowed to open degree essence of presented aproximation and define a linear differential equation, which deciding is it.

В работe [1,c.9], для аппроксимации событий, предшествующих катастрофе, предложено следующая функция от времени:

(1)

которая, по-видимому, обусловлена коллективным поведением одного и того же типа.
В настоящей заметке мы попытаемся указать простое дифференциальное уравнение, решением которого является функция, описываемая формулой (1).
Для этого преобразуем формулу (1) к виду:

или

Введём обозначение

Тогда

или

Введём в рассмотрение комплексную величину

(2),

реальной частью которой, в частном случае, является функция .
В общем случае сюда можно добавить конечное или бесконечное число степенных функций. Эта функция называется степенным полиномом её исследование вводит нас в степенную геометрию [2],[3].
Введём замену переменных

Тогда получаем простую формулу

(3)

с комплексными параметрами, где

может быть названо линейным временем в отличие от экспоненциального времени, описывающего соответствующий нелинейный процесс. [4]
А уравнение, которому удовлетворяет это решение, - это простое линейное дифференциальное уравнение второго порядка в линейном времени.

(4)

Это же уравнение может быть представлено в форме системы линейных уравнений первого порядка с двумя неизвестными

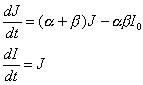(5)

Полный качественный анализ решений этой системы выполнен в классических учебниках по дифференциальным уравнениям [5].

Комплексификация аппроксимационной формулы и замена переменных позволили вскрыть линейную сущность представленной аппроксимации и предложить её обобщение с целью определения всё более мелкомасштабных мод катастрофических событий.

Литература
1.Управление риском. Риск. Устойчивое развитие. Синергетика.
М.: "Наука"2000.432с
2. Басин М.А. Спиральные числа. Степенные особенности. Волны. Вихри. Грибовидные структуры. Транспортно - информационные системы. Международная междисциплинарная научно-практическая конференция: "Современные проблемы науки и образования". Керчь, 27 июня - 4 июля 2001года. Материалы конференции .Часть1. Харьков 2001. С.12-13.
3.Брюно А.Д. Степенная геометрия в алгебраических и дифференциальных уравнениях. М.: Наука. Физматлит. 1998. 288с.
4. Басин М.А. Компьютеры. Вихри. Резонансы. Волновая теория взаимодействия структур и систем. Часть 2. Санкт -Петербург: "Норма" 2002. 144 с.
5. Арнольд В.И. Обыкновенные дифференциальные уравнения.Изд.3, перераб. и доп. -М.: "Наука" 1984.272с.