Ph.D . (Physics & Mathematics), Professor, Department  
Head M. V. Keldysh Institute of Applied Mathematics)
                  gmalin@spp.keldysh.ru                   

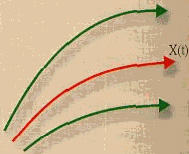Fig. 1. Any dynamic system describes a trajectory in the phase space, for example, such as that is shown in red. Dynamic chaos is conditioned by the fact that the adjacent trajectories (in green) are moving away from it. That is why some unimportant causes can have far-reaching consequences.

In 1963, Ray Bradbury published a science fiction story in which he formulated the concept of dynamic chaos. In this story, one of the organizers of an election campaign, after his candidate's victory, sets off on a voyage in time. The firm organizing these voyages offered hunts of dinosaurs that were destined to die in the near future. In order not to upset the complex fabric of genetic relationships, and not to alter the future, one had to follow specially identified paths. The hero, however, failed to stick to this rule, and accidentally crushed a golden butterfly. On returning, he found changes in the composition of the atmosphere, the rules of orthography, and the results of the elections. A tiny movement upset the smallest domino, and that upset a larger piece, until, finally, the fall of a gigantic piece resulted in catastrophe. The deviations from the initial trajectory caused by the crushed butterfly increased abruptly (See Figure 1). Small causes can lead to large consequences. Mathematics calls this property, sensitivity to initial data.
In the same year, Richard Feynman, also a Nobel Prize winner, formulated an idea on the limitation, in principal, of our ability to predict (or, as it is known today, on the existence of a prediction horizon or limit) even in our world, which is ideally described by classical mechanics. The existence of the prediction horizon does not necessitate "a God playing dice", adding some random members into the equations describing our reality. There is no need to sink to the level of the microworld, in which quantum mechanics offers probabilistic descriptions of the Universe. Objects whose behavior we are unable to forecast for sufficiently large periods of time can be quite simple: for example, the far from intricate systems of pendulums with small magnets that are on sale today in many shops, and referred to as works of "dynamic art".
The American meteorologist Edward Lorentz came to an understanding - also in 1963! - that sensitivity to initial data leads to chaos. He was bewildered by the question: why the sky-rocketing developments in computers did not lead to the realization of the wish of all meteorologists - reliably medium term (2-3 week) weather forecasts? Edward Lorentz proposed the simplest model for describing air convection (which plays an important role in atmosphere dynamics), ran it through his computer, and was bold enough to take the result seriously. The result was dynamic chaos: that is, non-periodic movements in determinate systems (meaning in systems in which the future is unambiguously defined by the past), possessing a finite prediction horizon.
From the point of view of mathematics, one can accept that any dynamic system, irrespective of the object it simulates, describes the path of a point in the space known as the phase space. The most critical characteristic of this space is its dimensionality or, to simplify this, the number of figures that are to be prefixed in order to determine the state of the system. For a mathematician or computer scientist, it is not at all important whether these numbers represent hares or lynxes in a certain territory, or variables describing solar activity, or a cardiogram, or the percentage of voters still supporting the president. If we accept that the point, on passing through the phase space, leaves a trace, then dynamic chaos would be represented by a tangle of trajectories, such as exemplified in Figure 2. In this case, the dimensionality of the phase space is only three. Is it not wonderful that such amazing objects exist even in just a three-dimensional world? Two other classic thinkers in non-linear science - D. Ruel and F. Tackens - in 1971 christened these tangles with a beautiful name -strange attractors.

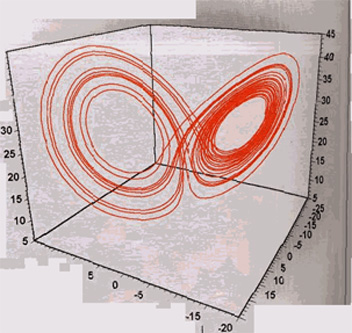Fig. 2. This computer-simulated image convinced E. Lorentz that he had discovered a new phenomenon -dynamic chaos. This tangle of trajectories, now called Lorentz's attractor, describes a non-periodic motion. Motion in this case does not become periodic, no matter how long we wait.

The individual models, computer experiments and observations, once put together, produce a fascinating picture. One can read, among the fragments of this mosaic, the prophecy of Henry Poincare - it will be possible some day to predict new physical phenomena on the basis of the general mathematical structure of the equations describing these phenomena. Well, computer experiments have transformed this dream into reality.
Another fragment - the endeav- is-ors of theorists that substantiated statistical physics and 35-discussed the question: why is it possible to use probabilistic language for describing not only movement, but dynamics as well. An important element of the mosaic is offered 15 by synergetics or non-linear dynamics, which came to life in the 1980s as an interdisciplinary approach.
Dynamic chaos made it possible, in a number of cases, to diagnose serious illness from electrical activity data using relatively simple computer software. Economic forecasts based on such notions as chaos and strange attractors even became a branch of industry!
A tremendous achievement - the development of a scenario for the transition from order to chaos. Irrespective of the equations describing a system, there are but few universal scenarios in our world. They do not depend on whether we open a water cock and observe the ordered smooth flow being transformed into a chaotic turbulent flow, or we pour a solution into a test tube in which a chaotic chemical reaction is under way, which gives us the pleasure of observing the play of colors. Behind all this multiplicity there is an intrinsic unity.

Since we find ourselves in a cul-de-sac and are striving to find a way out, it is natural to take a look at the landscape from above. All talk about stable evolutions indicate that mankind is exactly there. Well, let us ask ourselves: what does society expect of fundamental science in the 20th century?
It may be that the sad prophesy of E. Wiener, one of the fathers of quantum mechanics, has come true: science had a beginning, and it will also have an end. And the end will come soon. First, the next generation of fundamental theories will be of no interest to an increasing number of people. Secondly, because we failed to design a fundamental "building" for science, in which all the stories, secluded spots, cellars, and lofts are somehow connected with one another. It would be good to know that when one is in one part of the building, one could if necessary reach any other part. But this is still not possible.
Evolution offers many advantages over revolution. Therefore, we should predict the forthcoming changes, and be ready for them. Marie Antoinette was reproached by her mother because she did not expect any abrupt turns in society, such as revolution. It is important to say that the present generation of scientists, including those involved in the "non-linear approach" to the development of nature, does not deserve such a rebuke. Computer technologies have enabled huge databases to be created. The only problem is what should be done further with the majority of them. The most important thing is that these databases could be involved not only in the present-day computer business, but also in the principal game that our civilization is now playing.
In the 21st century, scientists will face a key problem, which can be called neuroscience. Neuroscience deals with consciousness, perception, and the intellection of the human being. This branch of science is at the interface between computer science, cognitive psychology, neurobiology, and non-linear dynamics. Chaos plays an extremely important role here. The brain, as well as many other systems of the human organism, works in a random mode. The recent theory of control over chaos suggests that it provides great scope for new approaches. In addition, specialists in non-linear dynamics try to involve encephalograms. But this is only a shadow of the successes that will be required in the future.
Another key problem to be solved by 21st century science is, conditionally speaking, the theory of risk and safety. Scientists faced this superproblem fifteen years ago, although it was forecasted to appear in the 1960s by Polish writer Stanislav Eem, in his book titled "The Sum of Technology".
We are living in a technological civilization, based on technology, not on theology as it was in the Middle Ages. All we need is to learn how we should handle this instrument with care and efficiency.

About thirty years ago, Richard Feynman was asked: "If all the living physicists died tomorrow, and only one phrase describing the Universe could be left for future generations, what should it say?" - "The Universe consists of atoms and a vacuum," Feynman answered. - "This description is sufficient and exhaustive. They will hit upon all the rest."
If present-day scientists, not only physicists but from any branch, were asked the same question, the phrase would have to be different: "Eearn to control risks." Controlling risks - this is one of the major technologies of our civilization. In general, the main path of the world's development is to exchange one threat or danger for another. It was obvious only recently that ideas of non-linear dynamics were intimately associated with the concept of risk control. This link became clear when paradoxical statistics on accidents were analyzed in detail. Let's recall the "Titanic", Chernobyl, Trimail, Bhopal... Each of these great disasters of the 20th century is related to a set of reasons and results, which are called "unfavorable coincidence of many improbable and rare circumstances". How can these random circumstances be described via a mathematical model? 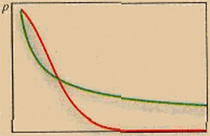Karl Gauss, who was called the king of mathematicians by his contemporaries, established that the sum of independent, equally distributed random parameters obey certain laws. The corresponding normalized curve is shown in Figure 3. As can be seen, the curve descends very fast. According to this law, large deviations occur very rarely. Hence, they can be ignored.
There is another class of laws that are called exponential laws (red curve in the same figure). In this case, the "tail" descends much slower - for this reason, these laws are called "distributions with heavy tails". Here, great deviations cannot be ignored.

Fig. 3. The Gaussian Distribution (shown in red) is considered to be classic and traditional. Following it, considerable deviations are so rare in occurrence that they can be neglected. However, many disasters, accidents, or debacles form statistics with exponential distributions (shown in green). In this case, infrequent disastrous events cannot be neglected.

What is the origin of exponential laws? In 1978, the American explorers P. Buck, C. Chang, and K. Weisenfeld put forward a simple hypothesis: an occasional impact in interactive dynamic systems can cause an avalanche to appear, similar to the case when dominos upset each other.
The source of danger lies between dynamics, which we mentioned at the beginning of this article, and an occasional event introduced from the outside world: as is said now, at the edge of chaos. This laid the foundation for a new star in non-linear dynamics: the theory of self-organized criticality. This theory can be applied to the behavior of stock markets, biological evolution, earthquakes, traffic highways, computer networks, and many others.
When scientists specializing in the study of chaos, computer simulation, and operation with large databases worked on the theory of controlling risks, they faced another interesting problem, which can conditionally be called the analysis of long relationships of reasons and results.
One can approach the problem of risk control based on work on information with the use of computer technology and global telecommunications. First, one should make a conclusion after every disaster, taking it as a lesson. All the disasters in the 20th century had forerunners, i.e. similar emergencies of he same type, but with less catastrophic effects.

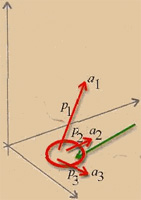Fig. 5. The picture evolved from problems related to the ruin of a bank. The small red area corresponds to the joker area, in which much care should be taken to avoid troubles.

Thus, to prevent the "premiere", one should make conclusions based on a small-scale "rehearsals," and in keeping with this approach, change standards, plans, and rules of the game applied to social life and the technosphere. The investment of one thousand dollars in the forecast and prevention of an accident is better than one million in liquidation of the consequences. Secondly, information and forecasting reduce the time required to respond to events, and hence allow many thousands of lives to be saved. Third...
However, it would be better to stop at this point. The Institute is engaged in very promising work, in which Chaos plays a key role.
Let's return to dynamic chaos, and ask ourselves: if the task of prevention of disasters is a considerable challenge, even with the use of modern computer technologies, how can we orient ourselves in this complex and rapidly changing world? How can we solve problems that can hardly be forecasted?
A new theory of channels and jokers tries to answer this question, and also to obtain the algorithms for forecasting.
This theory was developed, among others, by the well-known financier G. Soros. In his book "The Alchemy of Finances," he put forward the idea of an "informational" or "reflexive" economy. According to the theory, a set of variables such as "level of confidence", "expected profit", and many other parameters characterizing our "virtual reality" play a key role in the modern economy. These parameters allow one to create and destroy great financial pyramids. But exactly these parameters can vary stepwise, which is not typical of mathematical models simulated in the natural sciences.
In other words, in life we deal with a number of items composing a phase space, in which there are other spots called joker's areas. Any occasion or element of a game, or any factor that is absolutely unimportant in any other situation, can play a key role in the joker's areas. This not only can considerably affect the destiny of the system, but also transfer it in a stepwise manner to another point of the phase space. The rule, according to which the jump is made, is called the joker. This title comes from gambling -the Joker is a card that can be assigned the value of any other card at the player's wish. Undoubtedly, this rule drastically increases the number of variants and the degree of uncertainty.
Here's a simple example. Let's say we have a small bank. The financial situation worsens every day; an epoch of crisis presents no other alternative. It is now time to make a decision. First, the most natural (probability pi, See Figure 5): to organize a presentation at the Hilton hotel. This can cause a stir - an influx of journalists, and then new clients and opportunities. The second possibility: be honest enough to declare bankruptcy (probability p2). The third way: escape from the country with the rest of the bank's capital in cash, taking care of only family and close friends, and living abroad (this is a lesson from the Russian reformers - probability p3). So we face again a symbiosis of dynamics, predestination, and occasional coincidence.
This case can be reworded in terms of medicine. When one is located a long distance from the joker, the best results can be obtained from therapy. But location in the area of the joker calls for a surgeon's attention. Thus, the situation can be changed rapidly and considerably.
Dynamic systems can also be considered using the same approach. The picture shown in Figure 6 was designed by I. Feldshtein, a research fellow of the M. V. Keldysh Institute of Applied Mathematics of the Russian Academy of Sciences. This is again the Lorentz system. The colored arrows in the figure depict the speeds of divergence (the area over zero-level) or convergence (the area under zero-level) of the trajectory. As can be seen, the divergence area that naturally should be compared to the joker is rather small.

Fig. 6. Local speeds of divergence (convergence) for the Lorentz attractor. The areas above zero-level correspond to divergence, and under the zero-level, convergence. As can be seen, the first areas occupy a relatively smal part of the image.

If we fail to forecast the situation relative to the joker area, it could be that we will be fortunate enough to forecast something else. Let's consider: what does it mean that we are fortunate to forecast something? It implies that the behavior of the system is determined by only a few variables with the accuracy we need, and any other parameters in the first approximation can be neglected. In addition, we are able to predict the situation for a long enough period. These areas, belonging to the phase space, are called channels. Most probably, our ability to separate the channels effectively in the phase space and perfect the forecasting system, and common sense, gave us an advantage over other animals, rather than use of the trial-and-error method. We may approach the problem more widely: different theories, approaches and sciences can find a wide utility and demand, when they have successfully found the channels. Science is the art of simplification, and simplification can be achieved when one deals with channels. Certainly, "on the average", "generally", we cannot take a look beyond the horizon of the forecast. But "in particular", when we find ourselves in the range of parameters corresponding to the channel, and realize this fact, we can act reasonably and with caution. The problem is: where is the origin and the end of a channel? What is the structure of our ignorance? When we reach the end of a channel, how can we transfer from one information field and point of view, which corresponds to the previous channel, to others? Facing various economic, psychological, or biological theories, we imply, without necessarily keeping it in mind, that the developers of these theories dealt with different channels. The same situation exists in quantum mechanics, where the answer to the question, is the electron a wave or a particle, depends on the particular experiment.
At a conference on artificial intelligence, the following definition of the problem was presented. Simple problems are those that can be easily solved, or prove to be irresolvable; all other problems are complex ones. The development of our notion of chaos, and application of this approach to various problems, proves that we were lucky. Designing the future, comprehending a new reality, human nature, and algorithms of development and control has turned out to be a complex problem.