В работе предлагается динамическая модель развития транспортной сети. Основной особенностью модели является то, что развитие транспортной сети не является процессом централизованного решения задачи оптимизации перевозок, в ней рассматривается как результат самоорганизации на основе потребностей в перевозках товаров и развития инфраструктуры узлов сети. Тем не менее, в модели учтена возможность мягкого регулирования направлений развития моделируемой сети.

Проблема моделирования транспортных перевозок, проектирования и организации функционирования транспортных сетей далеко не нова. Достаточно упомянуть, что ее исследование привело к появлению целой отдельной области знаний – логистики [1].

Однако большая часть существующих моделей транспортных систем ориентирована на решение одного и того же, пусть и крайне важного, вопроса о построении оптимального в том или ином смысле плана перевозок. В таких моделях подразумевается, что все функционирование транспортной сети управляется из одного центра. При этом либо решается просто задача оптимизации перевозок в рамках существующей неизменной сети (например, [2]), либо изменения в структуре транспортной сети, ее развитие также рассматриваются как результат принятия некоего решения центром управления транспортной сетью и реализации этого решения [3], [4].

Между тем, в условиях наличия большого количества хозяйствующих субъектов эти предположения нельзя считать верными. В этом случае и схема перевозок, и процесс развития транспортной сети складываются из одновременных независимых друг от друга действий этих субъектов. При этом действия не являются ни полностью скоординированными, ни совершенно случайными.

Предлагаемая модель является попыткой описать на языке математики процесс самоорганизации (возникновения и развития) транспортной сети, происходящий не на основании некоторого единого плана, а самопроизвольно складывающийся при заданных географических условиях и параметрах спроса и предложения нескольких видов товаров.

Основной идеей модели является введение для каждого вида товаров величины, названной потенциалом. Потенциал численно характеризует потребность в данном товаре, существующую в данном узле транспортной сети. Именно разность потенциалов между узлами и создает в модели потоки товаров. Поэтому данный подход можно назвать «электромагнитной» моделью по аналогии с «гравитационными» моделями, уже достаточно давно использовавшимися в моделировании процессов с участием человека, а в последнее время применявшимися и для моделирования транспортных сетей [5].

Другим основанием для такой аналогии служит то, что темпы развития узла в модели полагаются пропорциональными квадрату потока товаров, перевозимых через данный узел. Это вызывает ассоциации с законом Джоуля-Ленца, описывающим количество тепла,. выделяемого при прохождении электрического тока через проводник. Разумеется, данная аналогия, как и любая другая, является весьма условной, поскольку в данной модели рассматривается «протекание» не через «проводник», а через узел. Итак, рассмотрим «электромагнитную» модель транспортной сети.

Модель представляет собой полный граф, каждой вершине и каждому ребру которого приписан определенный набор параметров и переменных. Вершины моделируют населенные пункты и характеризуются следующими величинами

1. Размер узла V i .
2. Выпуск продукции вида k P ik (отрицательное значение означает спрос на продукцию).
3. Потенциал продукции каждого вида j ik

Ребрам графа, изображающим транспортные коммуникации, связывающие населенные пункты, поставлены в соответствие следующие величины:

1. Длина L ij >0
2. Коэффициент затрат на расширение Q ij
3. Пропускная способность W ij ? 0
4. Поток продукции вида k S ijk .

Кроме этого, модель характеризуется глобальными параметрами «коэффициент проторенного пути» N > 1 и «коэффициент роста узлов» G > 0 . Первый из них показывает, во сколько раз затраты на прокладывание новой дороги с некоторой пропускной способностью превышают затраты на расширение существующей дороги на ту же величину.

Описываемая модель была реализована в целочисленном приближении, то есть все величины, кроме коэффициентов Q ij , N , G могли принимать только целые значения.

Начальное состояние модели задается набором значений V i , P ik , L i j, Q ij , W ij и глобальных параметров. Изменение состояния модели является пошаговым.

На каждом шаге методом последовательных приближений устанавливаются значения j ik и S ijk , исходя из условий:

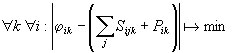(1)

(2)

Следует отметить, что в модели не требуется равномерного выполнения условий (1), минимизация осуществляется по каждому продукту, в порядке заданной «значимости» продуктов.

Установление маршрутов перевозки товаров происходит спонтанно, приоритет отдается маршрутам между вершинами с наибольшей разностью потенциалов для данного вида товаров. Если для данного ребра при достижении условия (1) итерационный процесс останавливается из-за нарушения условия (2), будем говорить, что имеет место перегрузка ребра.

После этого осуществляется изменение параметров вершин и ребер. Размер вершин является также динамической величиной и меняется в зависимости от уровня потока товаров через данную вершину.

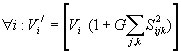(3)

При изменении размера вершины выпуски продукции всех видов в этой вершины изменяются пропорционально.

Для всех ребер, на которых возникла перегрузка, проверяется возможность увеличения их пропускной способности. При выполнении условия

(4)

осуществляется увеличение пропускной способности ребра

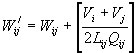(5)

В случае, если изначально пропускная способность ребра равна 0 (дорога отсутствует), приведенные формулы модифицируются следующим образом:

	(4а)
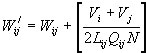	(5а)

К настоящему времени при помощи данной модели проведены лишь пробные расчеты. Наиболее интересным кажется расчет ситуации, в которой рассматривались четыре города (условно для географического соответствия выбраны названия Тверь, Иваново, Тула и Рязань), с начальным размером 100, производящие и потребляющие 4 вида товаров (каждый из городов производит один вид товара и потребляет три остальные), а также один город меньшего размера (20), не производящий продукции, но удачно расположенный на пересечении потенциальных торговых путей (Москва). В начальный момент дорог между городами нет.

Начальная конфигурация показана на рис. 1.

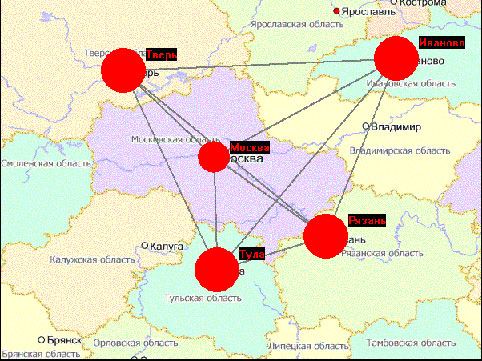
Рис. 1. Начальная конфигурация. Дороги еще не проложены.

Затем на протяжении 45 шагов (лет) происходит развитие транспортной сети. Поначалу новые дороги связывают только города-производители, которые растут за счет торговли. В приведенной на рис. 2 конфигурации размер каждого из четырех городов составляет около 150, рост Москвы не наблюдается.

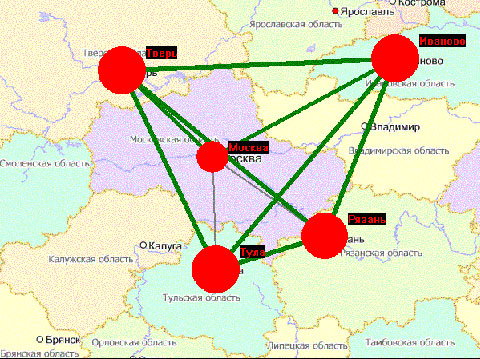
Рис. 2. четыре города активно торгуют между собой, начинается строительство дорог в направлении «неперспективной» Москвы.

Однако еще через 55 шагов ситуация резко меняется (рис. 3). Перевозчики товара «заметили» удобный перевалочный пункт. Строятся дороги, связывающие четыре города с Москвой, через которую направляется значительная часть потоков товаров и которая переживает бурный рост. В представленный момент размер Москвы достигает 250, в то время как размеры остальных городов едва превышают 200.

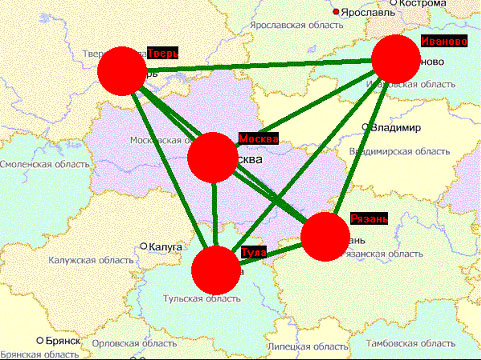
Рис. 3. Основные потоки товаров направляются через Москву, которая опережает остальные города в росте.

Ситуация будет выглядеть еще ярче, если вспомнить, что в модели формально заложен лишь рост городов, а при ее соотнесении с реальностью следует рассматривать относительные размеры узлов.

Представляется перспективным дальнейшее развитие модели и ее применение для прогнозирования и оценки перспектив развития реально существующих транспортных сетей.

Список литературы

1. Lucio Bianco, Agostino A Bella (eds.). Freight transport planning and logistics. Berlin etc.: Springer, 1967.

2. А . С . Бутов , Д . В . Гаскаров , А . Н . Егоров , Н . В . Крупенина . Под ред. А.С. Бутова. Транспортные системы. Моделирование и управление. СПб.: Судостроение, 2001. 552 с.

3. Попков Ю.С. и др. Системный анализ и проблемы развития городов. М.: 1983.