ЛЕКЦИЯ 3 Непрерывные модели: экспоненциальный рост, логистический рост, модели с наименьшей критической численностью. Модели с неперекрывающимися поколениями. Дискретное логистическое уравнение. Диаграмма и лестница Ламерея. Типы решений при разных значениях параметра: монотонные и затухающие решения, циклы, квазистохастическое поведение, вспышки численности. Матричные модели популяций. Влияние запаздывания. |
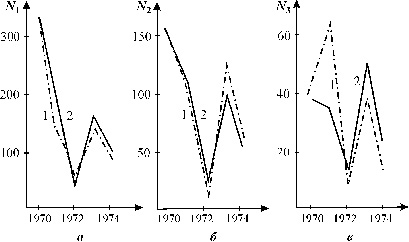
Численность популяции может меняться во времени различным образом: расти, совершать колебания, падать (рис. 3.1), и причины этого могут быть различны. Здесь мы рассмотрим модели роста популяций и математический аппарат, позволяющий описывать динамику численности разных популяций.
Уравнение экспоненциального роста.
Всемирно известной математической моделью, в основу которой положена задача о динамике численности популяции, является классическая модель неограниченного роста - геометрическая прогрессия в дискретном представлении,
|
|
(3.1)
|
или экспонента, - в непрерывном
| (3.2) |
Модель предложена Мальтусом в 1798 г. в его классическом труде "О законе роста народонаселения". Томас Роберт Мальтус (1766-1834) - известный английский демограф и экономист, обратил внимание на тот факт, что численность популяции растет по экспоненте (в геометрической прогрессии), в то время как производство
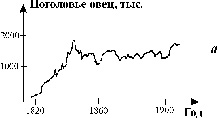 |
 |
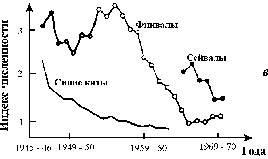 |
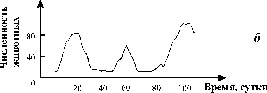
| Рис. 3.1. Примеры динамики численности популяций а - численность поголовья овец на острове Тасмания (Davidson,1938); б - изменение численности Daphnia magna (Frall, 1943); в - Динамика численности трех видов китов в Антарктике (приведена по изменению "индекса численности" убитых китов на 1 тыс. судо - тонно - суток, Gulland, 1971) |
питания растет со временем линейно (в арифметической прогрессии), из чего сделал справедливый вывод, что рано или поздно экспонента обязательно "обгонит" линейную функцию, и наступит голод. На основании этих выводов Мальтус говорит о необходимости ввести ограничения на рождаемость, в особенности для беднейших слоев общества. "Экономический пессимизм", следующий из прогнозов предложенной им модели, в основу которой положен анализ эмпирических данных, Мальтус противопоставлял модным в начале IXX века оптимистическим идеям гуманистов: Жана - Жака Руссо, Уильяма Годвина и других, предсказывающих человечеству грядущее счастье и процветание. Можно говорить о том, что Мальтус был первым ученым - "алармистом", который на основании результатов моделирования "бил тревогу" и предупреждал человечество об опасности следования развитию по используемым ранее сценариям прогресса. Во второй половине XX века такую "алармистскую" роль сыграли работы Римского клуба, и в первую очередь "модель глобального роста" Дж. Форрестера (см. Лекция 1).
Обсуждению важности вывода Мальтуса для популяционной динамики великий Дарвин посвятил несколько страниц своего дневника, указывая, что поскольку ни одна популяция не размножается до бесконечности, должны существовать факторы, препятствующие такому неограниченному размножению. Среди этих факторов может быть нехватка ресурса (продовольствия), вызывающая конкуренцию внутри популяции за ресурс, хищничество, конкуренция c другими видами. Результатом является замедление скорости роста популяции и выход ее численности на стационарный уровень. Модели ограниченного роста мы рассмотрим ниже. Что касается отбора, то в нем большое значение наряду с конкуренцией близких по своим потребностям особей играет территориальная изоляция, которая ведет к вымиранию близких форм и обеспечивает процесс дивергенции. Модели отбора мы рассмотрим в Лекции 7.
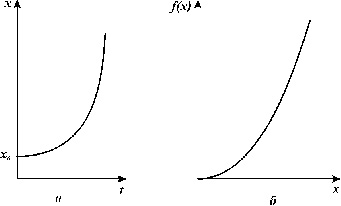
Вывод уравнения (3.2) рассмотрен нами в Лекции 2. График зависимости численности от времени в соответствии с законом экспоненциального роста изображен на рис. 3.2 а. На рис. 3.2 б. представлена зависимость скорости роста популяции (правая часть уравнения 3.2) от ее численности.
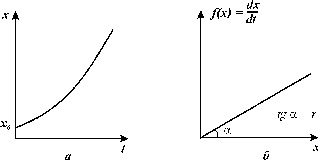 |
Рис. 3.2. Экспоненциальный рост. Зависимость скорости роста от численности (а) и численности от времени (б) |
В соответствии с экспоненциальным законом изолированная популяция развивалась бы в условиях неограниченных ресурсов. В природе такие условия встречаются крайне редко. Примером может служить размножение видов, завезенных в места, где имеется много пищи и отсутствуют конкурирующие виды и хищники (кролики в Австралии).
Ограниченный рост
Впервые системный фактор, ограничивающий рост популяции, описал Ферхюльст в уравнении логистического роста, рассмотренном нами в Лекции 2:
|
|
(3.3) |
 |
|
| Рис. 3.3. К определению величины К - емкости экологической ниши
популяции |
|
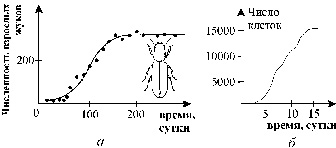
Логистическое уравнение обладает двумя важными свойствами. При малых зачениях х численность возрастает экспоненциально (как в уравнении 3.2) при больших - приближается к определенному пределу К.
Эта величина, называемая емкостью экологической ниши популяции, определяется ограниченностью пищевых ресурсов, мест для гнездования, многими другими факторами, которые могут быть различными для разных видов. Таким образом, емкость экологической ниши представляет собой системный фактор, который определяет ограниченность роста популяции в данном ареале обитания.
Уравнение (3.3) можно также переписать в виде:
|
|
(3.4) |
Здесь d - коэффициент внутривидовой конкуренции (за пищевой ресурс, убежища и т. п.) Аналитическое решение уравнения (3.3) мы получили в лекции 2:
|
|
(3.5) |
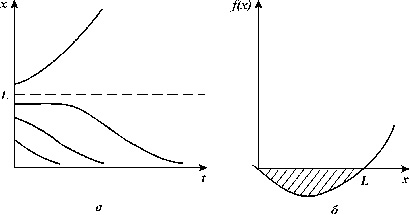
Формула (3.5) описывает кинетическую кривую, то есть зависимость численности популяции от времени. Ход кинетических кривых для разных начальных условий представлен на рис. 3.5.
В случае, если начальная численность меньше половины максимальной, кривая x(t) имеет точку перегиба с координатами
|
|
Ордината точки перегиба представляет собой половину максимальной численности,
а абсцисса зависит как от емкости популяции K, так и от константы собственной
скорости роста r ? чем выше генетические возможности популяции, тем скорее
наступает перегиб на кривой численности.
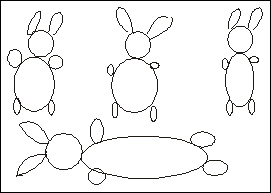
Примеры экспериментально наблюдаемой динамики популяций, развивающихся
по логистическому закону, приведены на рис. 3.4 а, б. На рис. 3.4 а сплошной
линией представлен график функции (3.5), при малых начальных численностях
он имеет S-образный характер.
При изучении более сложных систем мы не будем искать решение для x (t)
в явном виде, а ограничимся исследованием устойчивости их стационарных
состояний. Проведем такое исследование и для логистического уравнения.
Легко видеть, что уравнение стационарных состояний f (![]() ) = 0 в данном случае имеет два корня:
) = 0 в данном случае имеет два корня:
|
|
Посмотрим, будут ли эти корни устойчивыми. Для этого вначале воспользуемся
аналитическим методом Ляпунова. Введем новую переменную x, обозначающую
отклонение переменной х от ее стационарного значения:
x = ![]() .
.
Запишем линеаризованное уравнение для (3.4):
dx /dt = ax, где а = ![]() .
.
Напомним, что знак величины![]() определяет устойчивость соответствующей особой точки
определяет устойчивость соответствующей особой точки![]() :
:
|
|
(3.5) |
Подставив в выражение (3.5) значение первого корня![]() мы получим
мы получим![]() . Будем считать,
что величина r - коэффициент естественной скорости роста популяции положительная
. Будем считать,
что величина r - коэффициент естественной скорости роста популяции положительная![]() ;
- неустойчивая особая точка. Если же мы подставим в выражение (3.5)
;
- неустойчивая особая точка. Если же мы подставим в выражение (3.5)![]() то получим
то получим ![]() - отрицательную величину.
Это дает нам право утверждать, что стационарное решение уравнения
- отрицательную величину.
Это дает нам право утверждать, что стационарное решение уравнения ![]()
соответствует устойчивому стационарному режиму существования популяции
в ограниченной среде.
Проведем теперь исследование устойчивости стационарных решений этого уравнения,
исходя из графика функции правой части.
 |
| Рис. 3.4. Примеры ограниченного роста популяции. а - жук Rhizoretha
dominica в 10-граммовой порции пшеничных зерен, пополняемых каждую
неделю (Ccrombie, 1945). б ? Водоросль Chlorella в культуре (Pearsall,
Bengry, 1940)
|
 |
|
Рис. 3.5. Логистический рост. Зависимость функции правой части
f(x) - скорости роста от численности - для уравнения (3.3).
|
На рисунке 3.5 видно, что при переходе от отрицательных к положительным
значениям х в точке![]() = 0 функция
f (x) меняет знак с минуса на плюс, т.е. особая точка неустойчива. Наоборот,
в точке
= 0 функция
f (x) меняет знак с минуса на плюс, т.е. особая точка неустойчива. Наоборот,
в точке![]() = К имеет место изменение
знака f(x) с ростом x с плюса на минус, следовательно, эта особая точка
устойчивая.
= К имеет место изменение
знака f(x) с ростом x с плюса на минус, следовательно, эта особая точка
устойчивая.
Несмотря на схематичность положенных в ее основу представлений, логистическая
кривая оказалась очень хорошим приближением для описания кривых роста
численности многих популяций. В природе внутривидовая конкуренция не удерживает
естественные популяции на строго неизменном уровне, но действует в широком
диапазоне начальных значений плотности и приводит их к гораздо более узкому
диапазону конечных значений, определяя, таким образом, тенденцию к поддержанию
плотности в определенных пределах.
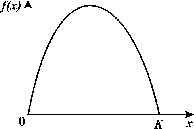
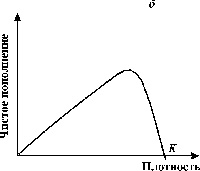
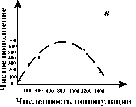
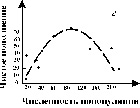
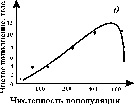
На рис. 3.6 показана схема расчета экспериментальных кривых пополнения. Разность между двумя кривыми (число рожденных минус число погибших) представляет собой число особей, на которое изменяется численность популяции в течение какой-либо стадии развития или за какой-нибудь промежуток времени. Пополнение популяции невелико при самых низких значениях плотности, возрастает по мере ее увеличения, снова снижается при достижении предельной плотности насыщения и становится отрицательным (смертность превышает рождаемость), когда начальная плотность превышает К.
Конкретный вид связи между скоростью пополнения популяции и ее плотностью меняется в зависимости от биологии вида (например, фазаны, мухи и киты на рис. 3.6 в, г, д). Поскольку скорость пополнения зависит от множества факторов, эмпирические точки никогда не ложатся точно на определенную кривую. Однако во всех случаях наблюдается колоколообразная кривая, форма которой отражает общую природу зависимых от плотности изменений рождаемости и смертности всякий раз, когда возникает внутривидовая конкуренция.
 |
 |
 |
 |
 |
|
Рис. 3.6. Кривые пополнения, соответствующие в модели кривым
зависимости скорости роста от численности популяции. а, б. - схема
расчета кривых пополнения, в, г, д - кривые пополнения для разных
видов:в - численность обыкновенного фазана на о. Протекши - Айленд после
его интродукции в 1937 г. (Einarsen, 1945);г - экспериментальная популяция плодовой мушки Drosophyla melanogaster
(Pearl, 1927); д - оценка численности арктического финвала (Allen, 1972) |
||
Модель популяции с наименьшей критической численностью
В рассмотренных моделях прирост численности (биомассы) популяции представлен линейным членом , пропорциональным численности. Строго говоря, это соответствует лишь тем популяциям, размножение которых происходит путем самооплодотворения (микроорганизмы). Если же в основе размножения лежит скрещивание, предполагающее встречи между особями разных полов одного и того же вида, то прирост будет тем выше, чем больше количество встреч между особями, а последнее пропорционально второй степени х. Таким образом, для разнополой популяции в условиях неограниченных ресурсов можно записать
|
|
(3.6) |
Уравнение (3.6) хорошо описывает тот факт, что при низких плотностях популяций скорость размножения резко падает, так как вероятность встречи двух особей разных полов уменьшается при понижении плотности популяции пропорционально квадрату плотности. Однако при больших плотностях популяций скорость размножения лимитирует уже не число встреч особей противоположного пола, а число самок в популяции, формула, учитывающая эти оба эффекта, имеет вид
|
|
(3.7) |
Графики численности в зависимости от времени (рис. 3.7 а) и скорости
размножения как функции численности (рис. 3.7 6) для уравнения (3.7.)
представлены на рис. 3.7.
В действительности плотность популяции не должна опускаться ниже некоторой
критической величины. При падении плотности популяции ниже критической
среднее время, в течение которого может состояться оплодотворение, становится
больше времени жизни отдельной особи, точнее времени, в течение которого
особь способна к размножению. В этом случае популяция вымирает.
 |
|
Рис. 3.7. а - график зависимости численности от времени и б
- скорости размножения как функции численности для уравнения 3.7
|
Этот эффект может быть учтен, если в формулу (3.7) ввести член, пропорциональный численности и описывающий смертность. Зависимость скорости роста популяции от ее численности при этом примет вид
|
|
(3.8) |
Уравнение (3.8) имеет два стационарных решения: ![]() =0
и
=0
и![]() = db (ab - dt) =L. Соответствующие
графики x(t) и f (x) даны на рис. 3.8, а, б. Из графика 3.8 ,б видно,
что решение
= db (ab - dt) =L. Соответствующие
графики x(t) и f (x) даны на рис. 3.8, а, б. Из графика 3.8 ,б видно,
что решение ![]() =0 устойчивое, а
=0 устойчивое, а![]() =L- неустойчивое. При начальных численностях xнач <L популяция вырождается,
х ® 0, причем тем быстрее, чем меньше xнач. Кривые x(t) при разных xнач
даны на рис. 3.8 а. При xнач >L в соответствии с уравнением (3.8) популяция
неограниченно размножается.
=L- неустойчивое. При начальных численностях xнач <L популяция вырождается,
х ® 0, причем тем быстрее, чем меньше xнач. Кривые x(t) при разных xнач
даны на рис. 3.8 а. При xнач >L в соответствии с уравнением (3.8) популяция
неограниченно размножается.
 |
|
Рис.3.8. Зависимость численности популяции от времени (а) и
скорости роста от численности (б) для уравнения (3.8). Штриховкой
обозначена область вырождения популяции.
|
Величина нижней критической плотности L различна для разных видов. Наблюдения биологов показали, что это всего лишь одна пара особей на тысячу квадратных километров в случае ондатр и сотни тысяч особей для американского странствующего голубя. Заранее трудно было предугадать, что столь многочисленный вид перешел через критическую границу своей численности и обречен на вырождение. Однако это произошло, несмотря на все усилия по охране этих птиц.
Для голубых китов критическая граница общей численности оказалась равной
десяткам - сотням. Хищническое истребление этих гигантских животных привело
к тому, что их осталось слишком мало в Мировом океане. И хотя охота на
них запрещена, надежд на восстановление популяции голубых китов практически
нет.
Наиболее общая формула, учитывающая как нижнюю границу численности, так
и внутривидовую конкуренцию, имеет вид
|
|
(3.9) |
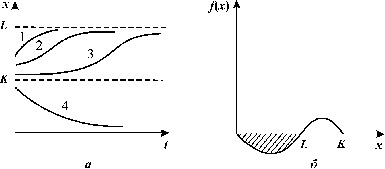
Зависимости численности от времени и скорости прироста от численности
представлены на рис.3.9 а, б.![]() =0 и
=0 и ![]() =К -устойчивые стационарные
состояния,
=К -устойчивые стационарные
состояния, ![]() =L - неустойчивое,
разделяющее области притяжения устойчивых состояний равновесия. Величины
L и К различны для разных популяций и могут быть определены только из
наблюдений и экспериментов. Ясно, что их определение представляет значительные
трудности. Кривые 1, 2, 3, 4 на рис. 3.9 а соответствуют различным начальным
значениям численности популяции.
=L - неустойчивое,
разделяющее области притяжения устойчивых состояний равновесия. Величины
L и К различны для разных популяций и могут быть определены только из
наблюдений и экспериментов. Ясно, что их определение представляет значительные
трудности. Кривые 1, 2, 3, 4 на рис. 3.9 а соответствуют различным начальным
значениям численности популяции.
 |
| Рис. 3.9. Зависимость численности популяции от времени (а) и скорости роста от численности (б) для уравнения3.9. Штриховкой обозначена область вырождения популяции. |
При любых промыслах особый интерес представляет величина нижней критической
границы, при переходе через которую популяция уже не сможет восстановиться.
Модель позволяет дать некий методический рецепт определения не самой критической
границы, но степени близости к ней численности вида.
Обратимся к рис. 3.9 а. Пусть численность вида в начальный момент времени
была близка к максимально возможной. При t = 0 происходит одноразовое
выбивание популяции. Если численность осталась значительно больше критической,
восстановление происходит сначала быстро, а затем с монотонным замедлением
(кривая 1). Если же оставшаяся популяция близка к критической точке, восстановление
происходит сначала очень медленно, численность популяции надолго "застревает"
вблизи критической точки, а затем уже, "набрав силы", более
быстро приближается к стационарному уровню (кривая 3). Кривая 2 представляет
промежуточный случай. Таким образом, наблюдая реакцию системы на возмущение,
можно предсказать приближение ее к опасным границам.
ДИСКРЕТНЫЕ МОДЕЛИ ПОПУЛЯЦИЙ
Численность популяции не изменяется непрерывно, а представляет собой дискретную
величину, что соответствует экспериментальным данным по переписи реальных
популяций. Если предположить, что численность N зависит от численностей
в некоторые предшествующие моменты времени, то для описания динамики численности
популяций можно применить аппарат разностных уравнений (отображений).
Если при этом внешние и внутренние факторы, определяющие развитие популяции,
остаются во времени неизменными, то численность популяции в момент времени
t может быть описана при помощи разностного уравнения в виде:
|
|
(3.10) |
Здесь функция F зависит от численности популяции в k предшествующие моменты
времени.
Особенно просто выглядит разностное уравнение в случае, когда численность
каждого следующего поколения в популяции Nt+1 зависит лишь от предыдущего
поколения Nt . Это справедливо для многих видов насекомых. Их взрослые
особи живут непродолжительное время, достаточное для откладывания яиц,
и к моменту появления на свет нового поколения (на стадии взрослой особи)
предшествующее поколение прекращает свое существование. То же имеет место
для некоторых видов зоопланктона, рыб, птиц. Про эти виды можно сказать,
что поколения в них не перекрываются во времени, и уравнение (3.10) может
быть записано в виде:
|
|
(3.11) |
Опыт показывает, что в таких системах при малых численностях N растет от одной генерации к другой, а при высоких - падает. Это свойство в экономике проявляется как закон "бумов" и "спадов".
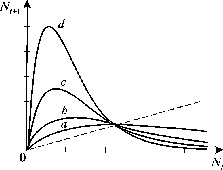 |
Рис. 3.10. Вид одноэкстремальной функции Nt+1=f(Nt). |
В таких случаях функция N - одноэкстремальная функция (рис. 3.10)
В зависимости от крутизны графика F (Nt) в системе могут возникать различные
режимы: монотонное и колебательное приближение к равновесию, колебательные
изменения - циклы разной длины и квазистохастическое поведение хаос.
Модели вида (3.11) являются простейшими детерминированными объектами,
демонстрирующими хаотическое поведение.
Если поколения перекрываются - появляются дискретные возрастные группы
(стадии развития). Для их описания обычно используются тоже дискретные,
но более сложные матричные модели.
Дискретное логистическое уравнение
Вспомним логистическое уравнение, которое описывает развитие популяции в непрерывном времени.
|
|
Заменим dN/dt на *N/Dt.
Здесь![]()
Получим:
|
|
(3.12) |
или Nt+1=Nt * f(Nt).
Однако, уравнение (3.12) биологически некорректно. Если в какой-то момент
времени значение численности становится больше определенной величины:
Nt>K(1+r)/r,
то уравнение (3.12) дает отрицательное значение Nt+1. Это связано с видом
функции f (Nt) (рис. 3.11 а).
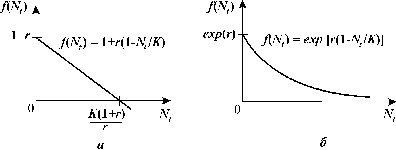 |
| Рис. 3.11. Вид функции для дискретного аналога логистического
уравнения: (а) - f(Nt)=r(1-Nt/K), (б) - f(Nt)=exp{r(1-Nt/K)}
|
Этот недостаток отсутствует у непрерывного логистического уравнения.
Чтобы исправить положение в дискретном уравнении, в качестве f (Nt) следует
взять функцию, асимптотически стремящуюся к нулю при Nt ® Ґ. Вид такой
функции изображен на рис. 3.11 б.
Экспоненциальная форма такой зависимости была предложена Мораном (1950)
для численности насекомых и Рикером (1952) для рыбных популяций:
|
|
(3.13) |
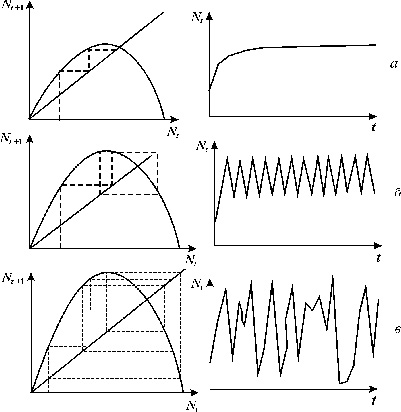
Ход решения можно наглядно продемонстрировать графически с помощью диаграммы и лестницы Ламерея. Точка пересечения биссектрисы первого координатного угла Nt+1=Nt и функции F(Nt) определяет равновесное состояние системы, аналогичное стационарному состоянию дифференциального уравнения.
На рис. 3.12 б показан способ нахождения значений Nt в последовательные моменты времени. Пусть в начальный момент времени N=N0.. F(N0)=N1 задает значение численности в последующий момент времени t=1. Величина N1 в свою очередь определяет значение F(N1)=N2. И так далее. На рис. 3.12 б изображен случай, когда траектория сходится к равновесному состоянию, совершая затухающие колебания.
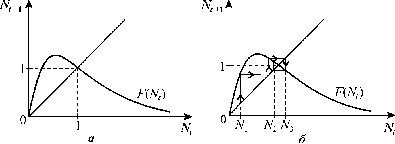 |
| Рис. 3.12. Определение равновесного состояния в дискретной модели
популяции с неперекрывающимися поколениями диаграмма (а) и лестница
Ламерея (б)
|
Введем для разностных уравнений (отображений) некоторые понятия, соответствующие основным понятиям теории дифференциальных уравнений.
Решение - (траектория) - любая последовательность значений {Nt}, (t=0,1...),
удовлетворяющая данному разностному уравнению при любом t. Разным начальным
значениям соответствуют разные решения.
Равновесием называется решение вида: Nt=const=N*, удовлетворяющее соотношению
N*=F(N*)
Как и в случае дифференциальных уравнений для исследования устойчивости
применим линейный анализ. Положим:
|
|
Линеаризуем уравнение (3.11) , разлагая F в ряд по степеням xt и отбрасывая
члены порядка и выше.
Получим:
|
|
Из условий сходимости геометрической прогрессии следует, что
xt ® 0 при t ® Ґ, если
|
|
(3.14) |
и xt ® Ґ при t ® Ґ, если
|
|
(3.15) |
Случаи ЅdF/dNЅ=1 и ЅdF/dNЅ=0 требуют дополнительного исследования членов
более высокого порядка в разложении.
Обозначим![]() .
.
В случае устойчивого равновесия:
при 0<A<1 ? отклонения от равновесия исчезают монотонно,
при -1<A<0 ? затухающие колебания вокруг N*.
Графики монотонного и немонотонного стремления численности к равновесному
состоянию в модели (3.13) представлены на рис. 3.13
В случае неустойчивого равновесия:
A>1 ? отклонение от равновесия монотонно растет,
A<-1 ? отклонение от равновесия в виде нарастающих колебаний.
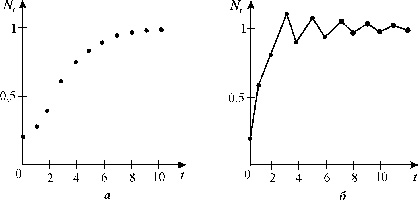 |
| Рис. 3.13. Графики численности популяции, вычисленные по формуле
(3.13) при выполнении условия (3.14).
|
Для уравнения (3.13) равновесие находится из выражения ![]()
Единственное равновесное значение N* = K>0 существует при любом r.
Равновесие устойчиво, если 0<r<2, решение монотонно при 0 < r
< 1 и представляет собой затухающие колебания при 1 < r < 2.
В уравнении 3.13 возможны и более сложные решения ? циклы, являющиеся
аналогом предельных циклов для систем дифференциальных уравнений (см.
лекция 8).
Решение называется циклом длины T, если
|
|
В уравнении (3.14) циклы (колебательное поведение переменных) наблюдается
при следующих значениях параметра:
при 2 < r = r2 < 2,526 - двухточечные циклы
при r2 < r < rc появляются циклы длины 4,8,16,...,2k.
При r>rc=3,102 решение зависит от начальных условий. Существуют трехточечные
циклы и квазистохастические решения.
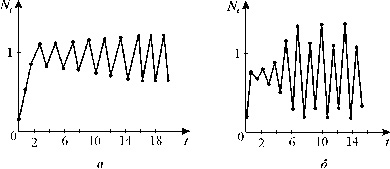 |
| Рис. 3.14. Циклическое поведение решения уравнения 3.13 а - двухточечный цикл, б - четырехточечный цикл.
|
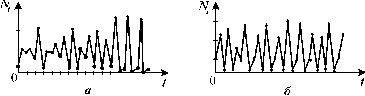 |
| Рис. 3.15. Примеры хаотических решений для уравнения 3.13 |
Иногда в качестве дискретного аналога используется более простая формула, в которой численность выражена в безразмерном виде. При Nt > 1 численность принимается равной нулю.
|
|
(3.16) |
На рис. 3.16 показаны диаграммы Ламерея и динамика численности во времени для разных значений параметра a в уравнении 3.16.
 |
|
Рис. 3.16. Диаграммы Ламерея и динамика численности во времени
для разных значений параметра a в уравнении 3.16. a - монотонный
рост; б - двухточечный цикл; в - квазистохастическое поведение
|
 |
|
Рис. 3.17. Области значений параметров для уравнения 3.17 с
различным характером поведения. Точками указаны значения параметров
для реальных
|
Аналогичными свойствами обладает уравнение
|
|
(3.17) |
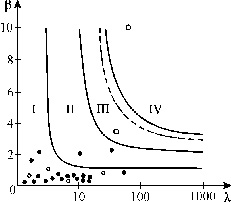
которое хорошо описывает динамику численности 28 видов сезонно размножающихся насекомых с неперекрывающимися поколениями (Hassel, 1976).
На рис. 3.17 показаны области параметров, где реализуются различные типы
поведения. Видно, что в стохастическую область попала лишь одна популяция.
Большинство популяций демонстрирует монотонный переход к состоянию равновесия.
Эти результаты наблюдений подтверждают правомерность использования в большом
числе случаев для описания динамики численности непрерывного логистического
уравнения.
Матричные модели популяций
Детализация возрастной структуры популяций приводит к классу моделей,
впервые предложенных Лесли, (1945, 1948).
Пусть ресурсы питания не ограничены. Размножение происходит в определенные
моменты времени ![]()
Пусть популяция содержит n возрастных групп. Тогда в каждый фиксированный
момент времени (например![]() , )
популяцию можно охарактеризовать вектор-столбцом
, )
популяцию можно охарактеризовать вектор-столбцом
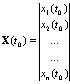 |
(3.18) |
Вектор X(t1), характеризующий популяцию в следующий момент времени, например, через год, связан с вектором X(t0) через матрицу перехода L:
|
|
(3.19) |
Установим вид этой матрицы. Из всех возрастных групп выделим те, которые
производят потомство. Пусть их номера будут k, k+1 ,..., k+p.
Предположим, что за единичный промежуток времени особи i-й группы переходят
в группу i+1, от групп k, k+1,..., k+p появляется потомство, а часть особей
от каждой группы погибает.
Потомство, которое появилось за единицу времени от всех групп, поступает
в группу 1.
|
|
(3.20) |
Вторая компонента получается с учетом двух процессов. Первый - переход особей, находившихся в момент в первой группе, во вторую. Второй процесс ? возможная гибель части из этих особей. Поэтому вторая компонента x2 (t1) равна не всей численности x1(t0), а только некоторой ее части
|
|
, |
Аналогично получаются третья компонента![]() и все остальные.
и все остальные.
Предположим, что все особи, находившиеся в момент t0 в последней возрастной
группе к моменту t1 погибнут. Поэтому последняя компонента вектора X (t1)
составляется лишь из тех особей, которые перешли из предыдущей возрастной
группы.
|
|
Коэффициенты для каждой группы имеют следующий смысл:
a - коэффициент рождаемости, b - коэффициент выживания. Вектор численностей
возрастных групп в момент времени t1 представим в виде:
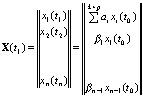 |
(3.21) |
Вектор X(t1) получается умножением вектора X(t0) на матрицу
 |
(3.22)
|
По диагонали матрицы стоят нули, под диагональными элементами ? коэффициенты выживания b, на первой строке стоят члены, характеризующие число особей, родившихся от соответствующих групп. Все остальные элементы матрицы равны нулю.
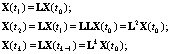 |
(3.23) |
Таким образом, зная структуру матрицы L и начальное состояние популяции
- вектор-столбец X(t0), - можно прогнозировать состояние популяции в любой
наперед заданный момент времени.
Главное собственное число матрицы L дает скорость, с которой размножается
популяция, когда ее возрастная структура стабилизировалась.
Пример популяции из трех возрастных групп (Уильямсон, 1967)
Пусть возрастная динамика популяции характеризуется матрицей:
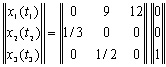 |
Такая запись означает, что исходная популяция состоит из одной самки
старшего возраста (вектор столбец в правой части уравнения). Каждое животное
старшего возраста, прежде чем умереть, успевает произвести в среднем 12
потомков, каждое животное среднего возраста, прежде чем умереть или перейти
в следующий возрастной класс (вероятности этих событий одинаковы) производит
в среднем 9 потомков. Молодые животные не производят потомства и с вероятностью
1/3 попадают в среднюю возрастную группу.
По прошествии одного временного интервала в популяции будет уже 12 самок
младшего возраста:
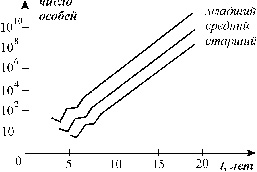 |
| Рис. 3.18. Численность самок старшего, среднего и младшего возраста в зависимости от времени для первых 20 временных интервалов (Джефферс, 1981) |
 |
Далее процедуру следует повторять на каждом шаге.
Из графика видно, что до некоторого момента времени (" t10), наблюдаются
колебания численности, после чего количество самок всех трех возрастов
экспоненциально возрастает, причем со-отношение между ними остается постоянным.
Главное собственное число l1 при этом равно 2, т.е. размер популяции за
каждый временной шаг удваивается.
 |
| Рис. 3.19. Динамика численности ценопопуляции овсеца Htlictotrichon
S. Для различных возрастных групп; а - проростки, прегенеративные
и генеративные особи, б - субсенильные особи, в - сенильные особи.
1 - эмпирические данные, 2 - прогноз по модели Лесли. (Розенберг,
1984).
|
Наклон графика равен ln l1 - собственной скорости естественного прироста. Соответствующий главному собственному числу собственный вектор отражает устойчивую структуру популяции и в нашем случае равен
|
|
Этот пример страдает тем же недостатком, что и модель Мальтуса экспоненциального роста: мы допускаем, что популяция может неограниченно расти. Более реалистическая модель должна учитывать, что все элементы матрицы L являются некоторыми функциями размера популяции.
Модели с применениями матриц Лесли для крупных возрастных групп могут дать описание колебательных изменений численности популяции. Пример такой модели ? описание динамики популяции овсеца Шелли ? мелкодерновинного злака северных луговых степей (Розенберг, 1984). Модель позволила описать наблюдаемые в природе явления - старение овсеца и колебания распределений по возрастному спектру в течение ряда лет (рис. 3.19).
Уравнения с запаздыванием
В реальных системах всегда имеется некоторое запаздывание в регуляции
численности, вызванное несколькими причинами. Развитие любой взрослой
особи из оплодотворенного яйца требует определенного времени. Поэтому
если какое-нибудь изменение внешних факторов, например, увеличение ресурсов,
вызовет повышение продуктивности взрослых особей, то соответствующее изменение
численности произойдет лишь по прошествии времени T. Это означает, что
уравнение
dx/dt=f(x),
где x - число взрослых особей в момент времени t следует заменить уравнением
dx/dt=f{x(t-T)}.
Логистическое уравнение с запаздыванием может быть записано в виде:
|
|
(3.24) |
Более точное уравнение, учитывающее распределение времени запаздывания имеет вид:
|
|
. (3.25)
|
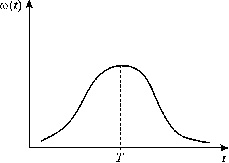
Типичный вид весовой функции w(t) изображен на рисунке 3.20. Такого типа
уравнения могут иметь колебательные решения. Это легко проверить для простого
линейного уравнения:
|
|
(3.26) |
Уравнение (3.26) имеет периодическое решение N(t) = Acos(pt/2T) в широком диапазоне значений скоростей роста r и времени запаздывания T.
 |
|
Рис. 3.20. Весовая функция распределения времени запаздывания
для уравнения 3.25
|
Решение уравнений с запаздыванием демонстрирует замечательное разнообразие динамических режимов, в том числе колебания и динамический хаос, в зависимости от значений параметров системы.
В технике хорошо известно, что запаздывание в регуляции системы может привести к возникновению колебаний переменных. Если система регулируется петлей обратной связи, в которой происходит существенная задержка, то весьма вероятно возникновение колебаний. (В экономике - причина бумов и спадов). Если продолжительность задержки в петле обратной связи больше собственного времени системы, могут возникнуть колебания с нарастающей амплитудой, нарушаются их период и фаза.
Принято считать, что малое запаздывание слабо сказывается на поведение системы. Однако в работах последних лет показано, что интуитивное представление о том, что чем больше запаздывание. тем больше его дестабилизирующий эффект, неправильно. В некоторых системах взаимодействующих видов оказалось, что малые времена запаздывания наиболее опасны для стабильности системы.
ВЕРОЯТНОСТНЫЕ МОДЕЛИ ПОПУЛЯЦИЙ
Рассмотренные нами модели популяций были детерминистическими. Однако существуют
два аспекта, по которым детерминистическая модель не может служить точным
отражением реальных экологических систем.
Во-первых, она не учитывает вероятностный характер процессов размножения и гибели; во-вторых, не учитывает случайных колебаний, происходящих в среде во времени и приводящих к случайным флуктуациям параметров моделей. Учет этих факторов приводит к существенному усложнению математического аппарата. Поэтому обычно исследователи стараются строить детерминистические модели, ограничиваясь упоминанием о возможных последствиях учета стохастики. Если детерминистическая модель свидетельствует об устойчивом равновесии, стохастическая модель предскажет длительное выживание. Если детерминистическая модель предсказывает периодические снижения численности одного или нескольких видов, стохастическая модель даст некоторую положительную вероятность вымирания этих видов. Наконец, если детерминистическая модель не выявляет равновесия или равновесие неустойчивое, стохастическая модель предскажет высокую вероятность вымирания.
Вероятностное описание процессов размножения и гибели.
В качестве простейшего примера рассмотрим вероятностное описание процесса
роста популяции с учетом только размножения. При детерминистическом подходе
мы считали, что существует определенная скорость размножения e такая,
что численность популяции п за время dt увеличивается на dn = en dt. Это
приводит к экспоненциальному закону
n = a ee t.
Здесь а - численность популяции в начальный момент времени. Подойдем к
процессу размножения с вероятностной точки зрения. Пусть вероятность появления
одного потомка у данной особи в интервале времени dt равна e dt. Тогда
вероятность появления одной новой особи в целой популяции за время dt
равна e n dt. Обозначим через p n (t) вероятность того, что в момент t
в популяции имеется ровно п особей. Предположим, что в каждый момент времени
может произойти только одно событие, а именно за время dt численность
популяции может либо увеличиться на 1, либо остаться неизменной. Размер
популяции в момент t можно связать с размером популяции в момент t + dt
с помощью следующих рассуждений. Если число особей в момент t + dt равно
n, это означает, что либо в момент t их было п - 1 и за время dt появилась
еще одна, либо в момент t было п особей и за время dt это число не изменилось.
Складывая вероятности, получим соотношение
| pn (t+dt) = pn-1 (t)e (n - 1) dt+ pn (t) (1-e) n dt, | |
|
(3.27)
|
или
|
|
(3.28)
|
|
|
(3.29)
|
Системы дифференциально-разностных уравнений, аналогичных уравнениям (3.27), которые можно рассматривать как динамические уравнения для случайного процесса, обычно бывает трудно разрешить в общем виде. Однако в нашем примере это довольно просто. Проинтегрируем уравнение (3.29) с учетом того обстоятельства, что ра (0) = 1. Это дает
|
|
|
|
В свою очередь этот результат подставляем в последующее уравнение, и весь процесс повторяется. После вычисления нескольких последовательных членов можно записать результат в общем виде:
|
|
(3.30) |
Выражение (3.30) определяет распределение вероятностей для любого момента
времени, заменяющее при вероятностном описании то единственное значение
которое рассматривалось в детерминистической модели.
Выражение (3.30) является частным случаем биномиального распределения.
Его математическое ожидание и дисперсия записываются следующим образом:
m(t) = a ee t , (3.31)
a2(t) = ae2et(1 - e-e t). (3.32)
Легко заметить, что математическое ожидание (3.31) совпадает с детерминистическим
средним. Таким образом, при большом числе особей детерминистическое описание
будет удовлетворительно заменять любую стохастическую модель, в которой
основное внимание уделяется нахождению средних значений. Когда же число
особей мало, например, когда начальный размер популяции составляет всего
лишь несколько единиц, дисперсия, т.е. среднее квадратичное отклонение
численности отдельно взятой популяции от математического ожидания, может
быть довольно значительной. При этом при t ® Ґ коэффициент вариации величины
п, равный s/ m, стремится к ![]() .
.
При рассмотрении какой-либо определенной популяции мы наблюдаем только одно численное значение. График роста обнаруживает значительные колебания. Возникает вопрос: каким образом эти колебания связаны с распределением вероятностей? Смысл выражения (3.30) состоит в том, что если имеется некоторое большое число популяций и в начальный момент времени t = 0 численность каждой из них равна а, то доля этих популяций, имеющих в момент t численность а, теоретически равна pn (t) с математическим ожиданием m(t) и дисперсией s2(t). Кривая роста любой отдельно взятой популяции может значительно отклоняться от соответствующей кривой математического ожидания, так что последняя вместе с дисперсией служит показателем случайной флуктуационной изменчивости, характерной для данного процесса.
Рассмотрим теперь более сложный процесс - размножение и гибель особей
в популяции.
Как и ранее, полагаем, что вероятность появления одного потомка у одной
особи в интервале времени Dt равна e Dt, поэтому для всей популяции вероятность
увеличения ее численности на единицу равна e n Dt. Допустим также, что
вероятность гибели одной особи составляет m Dt. Вероятность того, что
размер популяции в момент t+Dt составляет n особей, будет в таком случае
представлять собой сумму вероятностей трех событий:
- в момент времени t было n особей, и за время dt это число не изменилось;
- в момент t было n - 1 особей, за время dt их количество увеличилось на единицу;
- в момент времени t было n +1 особей, за время dt их количество уменьшилось на единицу. Выражение для pn(t +dt) принимает вид pn(t+dt)=pn-1(t)e(n-l)dt+pn(t)(1-endt-mindt)+pn+1p(t)e(n+l)dt, при n=l, 2,...
Эта система уже не решается простым интегрированием, однако применение метода производящей функции (Бейли, 1970) позволяет найти общее решение:
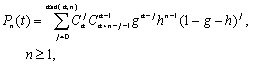 |
(3.33)
|
Таким образом, даже в случае простейшего стохастического процесса размножения
и гибели общее выражение для pn (t) оказывается довольно сложным, и выразить
его в явном виде, как правило, не удается.
Математическое ожидание и дисперсия распределения (3.33) имеют вид
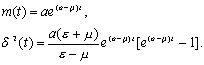 |
(3.34)
|
Как и в случае простого процесса размножения, математическое ожидание совпадает со значением численности в детерминистической модели, а выражение для дисперсии показывает, что имеет место значительная флуктуационная изменчивость.
Рассмотрим случай, когда размножение и гибель уравновешивают друг друга,
т.е. когда e = m. Математическое ожидание и дисперсию находим из формул
(3.34), полагая, что m ® e, и используя во втором выражении правило Лопиталя
для раскрытия неопределенности вида 0/0, получаем
m (е) = a,
s (t) = 2 a t.
Первое выражение представляет собой очевидный результат, а именно средний размер популяции сохраняет свое начальное значение. Второе выражение показывает, что дисперсия размера популяции возрастает пропорционально длительности интервала времени, в течение которого протекает процесс.
Детерминистическая модель в тех случаях, когда скорость размножения превышает скорость гибели, предсказывает устойчивое экспоненциальное увеличение размера популяции. Однако в вероятностной модели учитывается, что всегда существует определенная вероятность такого большого числа случаев гибели, при котором популяция полностью вымирает. Таким образом, вероятность вымирания является важной характеристикой вероятностной модели. Обозначим через p0(t) вероятность того, что в момент времени t не останется ни одной живой особи. Приравняв правую часть к нулю, из уравнений (3.33) можно найти выражения для этой вероятности в явном виде:
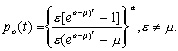 |
(3.35)
|
|
|
(3.36)
|
Вероятность того, что рано или поздно произойдет вымирание популяции, можно найти, полагая t ® Ґ. В пределе при t ® Ґ выражения (3.35) и (3.36) для случаев e < m , e = m, e > m можно записать следующим образом:
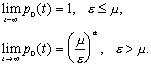 |
Следовательно, если скорость размножения не превышает скорости гибели, вымирание рано или поздно обязательно произойдет. Если же скорость размножения выше скорости гибели, то вероятность вымирания составляет (m./e) a.
Интересно, что в том случае, когда e = m и математическое ожидание численности имеет постоянную величину, вероятность полного вымирания все же равна единице. На самом деле в природе происходит следующее. Несколько популяций увеличиваются до очень больших размеров, тогда как большинство популяций вымирают, и в результате сохраняется некоторое постоянное среднее. Изучая эти наиболее многочисленные в биоценозе популяции, часто можно ограничиться их детерминистической моделью.
Учет флуктуаций среды.
Флуктуации условий среды могут приводить к изменению характера взаимодействий
между отдельными особями, т.е. случайному изменению параметров модели.
Для модели экспоненциального роста - это случайные изменения коэффициента
естественного прироста, учет которых приводит к уравнению
dx/dt = (e + y(t))x,
m(t)=aee t ,
|
|
где s2 - дисперсия y (t). Отсюда
|
|
Таким образом, с течением времени колебания численности популяции становятся более резкими; это значит, что детерминистическая система не имеет устойчивого стационарного состояния. Можно показать (Свирежев, Логофет, 1978), что при e < s2 вероятность вырождения со временем увеличивается, стремясь в пределе к единице - популяция вероятностно неустойчива, т.е. достаточно длительное воздействие возмущений с большой вероятностью может привести к ее гибели. При e > s2 вероятность вырождения уменьшается, и при t ® Ґ стремится к нулю - популяция в этом смысле устойчива.
Из полученного результата следуют более жесткие ограничения на коэффициент естественного прироста, чем из детерминистической модели. В самом деле, в последней для невырождения популяции достаточно, чтобы среднее значение коэффициента e было положительным, в то время как в стохастической модели этого недостаточно - нужно, чтобы e > s2.
Следствием учета случайных факторов в математических моделях теории популяций (и в теории биологических сообществ) являются более жесткие требования к параметрам системы, которые обеспечивают ее устойчивость. Область устойчивости, полученная по какому-либо критерию на основании стохастической модели, как правило, бывает у'же аналогичной области для детерминированной модели.
В целом видно, что детерминированная модель гораздо более проста и наглядна, но не дает сведений о том, насколько кривая роста той или иной популяции под действием случайных величин может на самом деле отклоняться от теоретической кривой, задаваемой этой моделью. Детерминистическая модель также не позволяет оценить вероятность случайного вырождения популяции. Однако, поскольку при возрастании численности случайные величины, характеризующие численности популяций, сходятся по вероятности к своим средним значениям, то поведение популяций с достаточно большой численностью удовлетворительно описываются динамикой средних величин. Поэтому для сообществ, численность которых велика, применимо детерминистическое описание.
Литература.
Базыкин А.Д. Математическая биофизика взаимодействующих популяций. М.,
Наука, 1985.
Бигон М., Харпер Дж., Таусенд К. Экология. Особи, популяции и сообщества.
М., Мир 1989
Ризниченко Г.Ю., Рубин А.Б. Математические модели биологических продукционных
процессов. М., Изд. МГУ, 1993
Свирежев Ю.М., Логофет Д.О. Устойчивость биологических сообществ. М.,
Наука, 1978
Leslie P.H. Some futher notes on the use of matrices in population mathematics.
Biometrica, v.35, 1948
Malthus T.R. An essay on the principal of Population . 1798 (Penguin Books
1970)
May R.M. When two and two make four: nonlinear phenomena in ecology. Proc.
R. Soc. London, B228, N1252, 241-268, 1986
Verhulst P.F. Notice sur la loi que la population suit dans son accroissement
Corr. Math. Et Phys. 10, 113-121, 18